CP-1002: Preliminary Modeling, Testing and Analysis of a Gas Tankless Water Heater

Introduction

Tankless water heaters (TWH) save energy primarily by eliminating the energy losses associated with a storage tank, and their market share is increasing (1). Pros and cons of TWHs generally are shown in Table 1, with energy savings (see Table 2) probably the key factor driving increased interest. Savings are most often estimated using published energy factors [EF ≡ Qt_{o load}/Q_in], which are measured at 64 gal/day usage with 6 draws of 10.6 gal each (2). Although reasonable for storage tank water heaters, using a few large draws unrealistically minimizes the impact of cycling of the heat exchanger mass with TWH. Each cool-down of that mass wastes a certain amount energy to the environment, and the more draws/per day there are, the more waste and inefficiency there is. Using an accurate simulation model will permit efficiency estimation for any draw pattern (e.g., that deemed best by a standards-making body). To make the simulation model accurate for a given unit while keeping the model simple, key model parameters should be derived from simple tests. In this paper, a model is proposed whose key parameters can be determined by tests which could be executed in under an hour.

Table 1: Pros and Cons of Tankless

^1. No hard data exists to support this reasonable conjecture.

Table 2: WH Energy Factors and Savings

1. Data taken from (2), except for condensing units

2. % savings = (EF_tnkls — EF_tank)/EF_tank

3. Emerging condensing gas units, not uet listed (2)

There are two types of TWHs: gas and electric. For wholehouse applications, systems are predominantly gas because of the high power demand. For example demand is more than 200 kBtu/hr (30kW) at 6 gpm with a 70°F temperature rise. Gas TWH have somewhat larger savings potential than electric TWH do, because conventional gas tanks with their central flue design are more inefficient to begin with (EF ~0.58) compared to electric storage-tank water heaters (EF ~0.92). Although all the modeling introduced here applies equally to gas or electric systems with minor parameter changes, gas dominates the whole-house tankless market (1) and is of primary interest here.

Savings from TWH are most often inferred from standard water heater tests (2). Typical EFs and estimation of savings are shown in Table 2. The test procedure specifies six equal draws of ~10.6 gal each, one hour apart, as in Fig. 1. The issue here is not with the total daily draw volume; 64 gal/day is a reasonable average. However, realistic usage invariably shows frequent small sink draws, as also shown in Fig. 1. This is of little consequence for storage water heaters, where the outlet temperature is mostly independent of draw volume, flow rate, and time (short of runout); but it is critical for tankless.

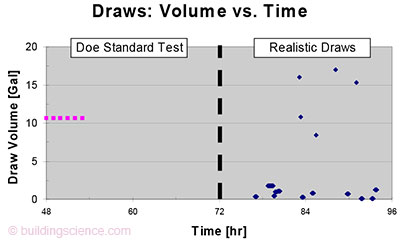
Figure 1: The standard test draw profile (left side), contrasted to a more realistic draw pattern (right side).

To analyze tankless efficiency, it is useful to define an efficiency for each draw:

η_draw=Qout/Q_in=[∫_drawdt(m_dotc_p(T_out–T_in))]/{∫_drawdtQ_dot,in}             (1)

(see Nomenclature, Section 7, for definition of terms). In the standard test (2), η_draw and the resulting EF are close to the burner efficiency η_burn, as the energy to charge up the heat exchanger is small compared to the draw energy. However, η_draw is much lower than the EF for small draws, as shown in Fig. 2 (3). Thus, actual long-term efficiency of a TWH depends on the details of the draw schedule and will be generally lower than EFs published at (2). Actual draw patterns are very complex, and no draw pattern is universally accepted; each standards-making body or study will want to make their own assumptions. In this paper, a model is proposed that will allow reasonably-accurate calculation of efficiency for any assumed draw pattern.

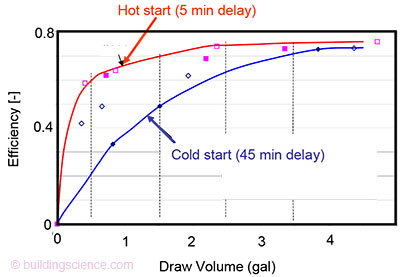
Figure 2: Draw efficiency versus the volume of the draw, for 5 min. and 45 min. delay. Adapted from (3).

Table 3: Key Gas Tankless Parameters

1. Data mostly from the tankless rating directory in (2).
2. Manufacturer’s data; the unit is currently not listed at (2).
3. For electric: η_birm ≡ 1, and EF > .99. For gas, condensing units with EF > 0.95 are recently available.
4. NM = Not measured, NK = not known
5. Applies to all gas and electric/discrete units.
6. Some TWH can vary continuously; others have discrete levels only.
7. Electrical power includes microprocessor, controls/sensors, and fan(s), in both on and off states

The model used here is shown in Fig. 3. It consists of a single lumped node for the heat exchanger and water mass, with coupling to T_env, draw loss, and gas input. In reality, there is a temperature gradient along the heat exchanger, and higher order models will likely be needed ultimately. An energy balance on the mass node yields the equation:

C dT/dt = ηQ_dot,gas – m_dotc_p(T – T_in) – UA(T – T_env)           (1)

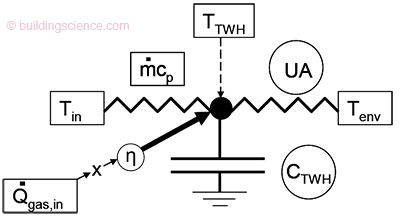
Figure 3: Tankless thermal circuit model. Variables in boxes are measured; parameters in circles are to be determined.

The modeling framework TRNSYS was used (4). Documentation of the tankless model can be found at (5). Constraints imposed on the model include: i) there is a userspecified delay after the draw starts before the burner ignites (~5 secs, for establishing fan flow and safety interlocks); ii) there is a minimum flow rate to actuate the burner (0.5-0.8 gpm); iii) there are minimum and maximum Q_dot (for gas, Q_dot,min is typically 10% to 20% of Q_dot,max). The time step is subdivided into constant-Qdot portions as needed whenever controls change burner setting, and averages are computed over the time-step.

Q_dot can be continuous or discrete. Controls for the discrete case use a “feedback + deadband” approach. At start of a time-step, if m_dot > m_dot,min, the burner was previously off, and (T_outset), Q_dot is set to Q_dot,max. If (T_out > T_set) occurs during the time-step, the burner is re-set downward one step. If (T_out>T_set) occurs at Qdot,min, then the burner is turned off. Then, when (T_outset-T_dband), the burner start cycle is reinitiated, with the concomitant delay. This will lead to large oscillations when T_in is too high, as described in Section 5 and in (3). TWH with feed-forward control anticipate and avoid this issue. Feed-forward units are not yet modeled.

New models should first be validated analytically insofar as possible. Fig. 4 shows the model response to varying flow rate, to compare to expectation. In region 1, there is decay from a previous firing toward T_env. In region 2, a draw is initiated with m_dotdot,min, and the unit does not fire. In regions 3 and 5, flow rate varies, with mdot > m_dot,min, and T_out is maintained at T_set. In region 4, the power needed to reach setpoint is above Q_dot,gas,max, and T_out sags down below T_set. The flow in region 6 is too low to fire the burner, and the cold mains water flowing through lowers T_out below T_amb. This leads to a rise in T_out toward T_amb in region 7. All this behaviour (and the time constants) is as expected.

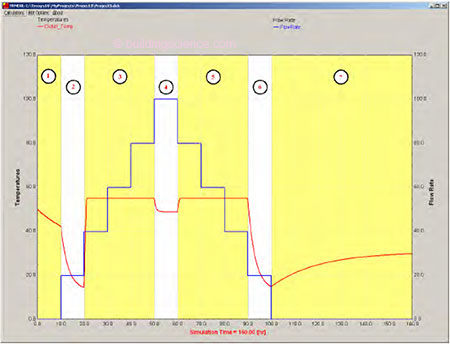
Figure 4: Model response to varying flow rates. The red line is T_out, and the blue line is m_dot,in. . .

Download complete document here.